- 3,133
hi
http://mrfizzix.com/autoracing/tiresgrip.htm
can anyone explain to me the phytagorean theorem there? i know what it is, but i don't understand why they use it....
quote:
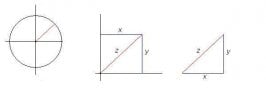
It is a circle centered on an x-y axis graph. The radius of the circle is 1 unit. 1 unit is equal to the adhesion limit of a tire. Thus, on the traction circle, .45-G of acceleration would be .5 graph units, since it is half the tire's limit. The y-axis represents acceleration and braking. The x-axis represents turning. Anyone who has basic geometry can find if the tire will slip or not using the traction circle. basically, if you have graph paper, you can just pinpoint the spot. For example, if you are using 1-G rated tires, and are accelerating at .5-G and are in a 15-m turn at around 20-mph (.5-G of lateral acceleration, see above) your tires should hold. To prove this mathematically, we can use the Pythagorean Theorem. Draw a right triangle with the horizontal leg representing lateral (turning) acceleration, and the vertical leg representing acceleration/braking force. Using the Pythagorean theorem we can find the hypotenuse:
R2 = x2 + y2
R2 = .52 + .52
R2 = .25+.25
R2 = .5
r = .71-units
:end quote :
i don't get it...... ><
http://mrfizzix.com/autoracing/tiresgrip.htm
can anyone explain to me the phytagorean theorem there? i know what it is, but i don't understand why they use it....

quote:
It is a circle centered on an x-y axis graph. The radius of the circle is 1 unit. 1 unit is equal to the adhesion limit of a tire. Thus, on the traction circle, .45-G of acceleration would be .5 graph units, since it is half the tire's limit. The y-axis represents acceleration and braking. The x-axis represents turning. Anyone who has basic geometry can find if the tire will slip or not using the traction circle. basically, if you have graph paper, you can just pinpoint the spot. For example, if you are using 1-G rated tires, and are accelerating at .5-G and are in a 15-m turn at around 20-mph (.5-G of lateral acceleration, see above) your tires should hold. To prove this mathematically, we can use the Pythagorean Theorem. Draw a right triangle with the horizontal leg representing lateral (turning) acceleration, and the vertical leg representing acceleration/braking force. Using the Pythagorean theorem we can find the hypotenuse:
R2 = x2 + y2
R2 = .52 + .52
R2 = .25+.25
R2 = .5
r = .71-units
:end quote :
i don't get it...... ><